La ciencia de las conexiones: los grafos y el estudio de la propagación
Esta rama de las matemáticas, con su aparente sencillez, ha demostrado ser una herramienta indispensable para modelar y analizar sistemas complejos. Desde las redes sociales y la web hasta la biología y la ingeniería, los grafos permiten visualizar, comprender y optimizar las relaciones entre diferentes elementos.
El proyecto del Dr. Adrián Pastine, docente del Departamento de Matemática de la FCFMyN e investigador asistente de CONICET, fue uno de los seleccionados en la Convocatoria de Proyectos de Investigación Inicial (PROINI) 2024 de la UNSL. La propuesta titulada “Problemas de propagación en grafos”, pretende buscar respuestas a algunos problemas que permitirían explicar cómo se contagia una enfermedad, o cómo se difunde un contenido en una red de comunicación.
La teoría de grafos tiene múltiples aplicaciones, su simpleza y versatilidad posibilita crear modelos matemáticos que contribuyen a visualizar una multiplicidad de temáticas. Pero ¿cómo se estudian estos problemas desde la investigación básica? En esta entrevista, Pastine explica qué se proponen estudiar y por qué.
Empecemos por explicar ¿qué es un grafo y cómo se representa?
Un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo. Los grafos son estructuras matemáticas utilizadas para representar relaciones binarias entre distintos objetos, donde los vértices representan a los objetos y las aristas representan la existencia de una relación entre dos objetos dados.
Estos objetos matemáticos permiten estudiar múltiples problemas como por ejemplo, problemas de conectividad, de robustez de una red y qué tan propensa es a sufrir ataques, o inconvenientes en un tendido eléctrico de una ciudad, entre muchas otras.
¿Qué son los problemas de propagación? ¿cómo se pueden explicar a través del empleo de esta teoría?
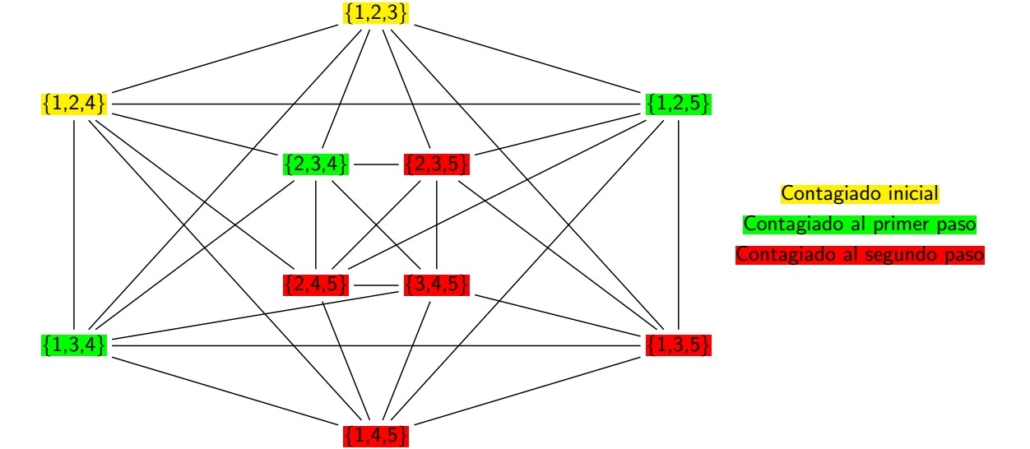
En este tipo de problemas se estudia cómo se propaga una condición dada en el grafo. En particular, para el problema en el que se centra este proyecto, suponemos que hay un conjunto inicial de vértices con una condición dada, y que otro vértice recibe la misma condición si dos de sus vecinos la tienen. Así, la condición puede ser una enfermedad (pensando en contagios en humanos), pero también puede ser un mensaje o una publicidad dadas (pensando en propagación de mensajes en redes sociales). Por ejemplo, la representación de redes sociales, en las que cada persona es representada por un vértice, y las aristas representan que estas personas se siguen en dicha red social.
Nos proponemos trabajar en una familia de grafos relacionados a los grafos de kneser. Esto se puede pensar como que los vértices de esos grafos son personas y tienen una arista que los une si comparten muchas cosas. Si nos centramos en el contagio de enfermedades, dependiendo de la cantidad de lugares en común que visitan como la oficina, el supermercado o el gimnasio, entonces una persona se puede contagiar si coincide en suficientes lugares con otras personas enfermas. También los grafos nos permiten estudiar la propagación de información, ya sea porque las personas visitan suficientes lugares donde hay otras personas que manejan esa misma información como pueden ser las redes sociales. Para poder explicitar los problemas de propagación, necesitamos introducir los conceptos de camino, distancia y diámetro. Estudiar estos cruces y relaciones, nos permite dar respuestas a estos problemas.
¿Trabajan con simulaciones?
La respuesta es sí y no. Hacemos simulaciones pensado en el grafo, pero sin anclarlo a un problema concreto. Eso nos permite plantear posibles soluciones o respuestas que después otros especialistas aplican a diferentes disciplinas.
¿Qué se proponen alcanzar con este proyecto?
El objetivo de este proyecto es hacer aportes originales al estudio de problemas de propagación en grafos y formar recursos humanos en esta línea de estudios para tener un impacto significativo en el eje temático de salud y en el de comunicación.
¿Quiénes integran el proyecto?
Lo integra el Dr. Daniel Jaume, la Lic. Agustina Ledesma, la Lic. Valentina Soltera, el Lic. Kevin Pereira y el Lic. Rodrigo Sota. También colabora gente de otras universidades, como el Dr. Pablo Torres de la Universidad Nacional de Rosario, el Dr. Luciano Grippo de la Universidad Nacional de General Sarmiento, el Dr. Mario Valencia Pavón de Francia, de la Université de Lorraine y el Dr. Fabio Protti de la Universidade Federal Fluminense de Brasil.