Nueva defensa de la Maestría en Matemática

La Lic. Marina Roldán defendió su tesis de posgrado para optar el título de “Magíster en Matemática” en el Departamento de Matemática de la Facultad de Ciencias Físico Matemáticas y Naturales.

Dicha tesis se tituló “Un Nuevo Concepto de Derivada. Aplicación a Mejor Aproximación Local”, dirigida por el Dr. Fabián Eduardo LEVIS y codirigida por el Dr. David Eduardo FERREYRA, ambos docentes del Departamento de Matemática de Facultad de Ciencias Exactas Físico Químicas y Naturales de la Universidad Nacional de Río Cuarto e investigadores del CONICET.

Los miembros del jurado fueron la Dra. Sigrid B. HEINEKEN (Universidad de Buenos Aires);  la Dra. Patricia M. MORILLAS (Universidad Nacional de San Luis) y el Dr. Daniel A. JAUME  (Universidad Nacional de San Luis).

De la defensa virtual también participó la Secretaria de Ciencia y Técnica / Posgrado de la FCFMyN, Dra. Verónica Gil Costa.

– ¿Cómo describe este momento al culminar su carrera de posgrado en la FCFMyN?

-Fue un momento muy esperado, tanto la defensa de la tesis como lo es la espera del título acreditante. Lamentablemente las condiciones de público conocimiento no permitieron que el encuentro pueda desarrollarse de manera presencial sino que la defensa de tesis fue virtual, lo que no quitó mérito a los nervios clásicos de ese último examen o a la emoción de culminar una carrera. Si es verdad que me hubiese gustado compartir ese momento con los jurados, director, codirector y colegas, pero la situación sanitaria no colaboró y pese a que la defensa fue virtual fue una experiencia muy gratificante.

– ¿Cómo se resume su tema de investigación?

El trabajo realizado se encuadra dentro de la rama del Análisis que contempla Teoría de Aproximación. Precisamente, los problemas abordados se conocen en la literatura como problemas de mejor aproximación local.

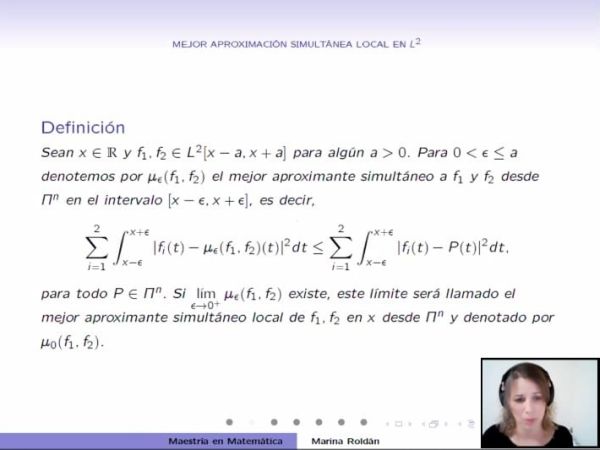
Habitualmente las técnicas usadas para el abordaje de este tipo de problemas se basaban en el estudio del comportamiento asintótico de los errores. Un hecho si se quiere natural, ya que las condiciones que se asumían sobre las funciones que uno consideraba eran establecidas sobre la norma de dichas funciones. En el año 2015, el Dr.David Ferreyra en su tesis doctoral, estableció nuevas condiciones suficientes para asegurar la existencia del mejor aproximante local de una función de los espacios Lp en un punto de la recta real, mediante el uso de técnicas diferentes a las conocidas. Más específicamente, introdujo un nuevo concepto de suavidad de una función, llamada la condición Cp, que permitió ampliar la clase de funciones de los espacios Lp para las cuales existía el mejor aproximante local. No obstante, las condiciones de diferenciabilidad asumidas establecían condiciones suficientes, pero no necesarias para la existencia del m.a.l. de una función en un punto. En nuestro trabajo abordamos el problema de mejor aproximación local para una función del espacio de funciones L2 en un punto de la recta real. En él, introducimos un nuevo concepto de derivada denominado derivada de Legendre que extiende la ya conocida condición C2.

En primera instancia analizamos la unicidad y propiedades de la derivada de Legendre así como también su relación con la condición C2. A continuación y haciendo uso de la derivada de Legendre caracterizamos la clase de todas las funciones en L2 para las cuales existe el mejor aproximante local y también caracterizamos la clase de todos los pares de funciones en L2 para los cuales existe el mejor aproximante simultáneo local. Además, analizamos una propiedad geométrica del conjunto de los puntos clausura de la red de los mejores aproximantes a una función cuando su dominio se reduce a sólo un punto. Finalizamos la tesis, con un resultado que describe el comportamiento asintótico de las redes de las primeras derivadas de mejores aproximantes bajo ciertas condiciones adicionales de suavidad.

– ¿Por qué decidió estudiar en la FCFMyN?

-Al finalizar los estudios de grado en Licenciatura en Matemática, tanto mi director como mi codirector de tesis me recomendaron estudiar la Maestría en Matemática y el Doctorado en Ciencias Matemáticas en la UNSL. En primera instancia porque conocían la institución, de hecho tanto Fabián como David son graduados de la misma, además de conocer la calidad de los docentes tanto como grupo de trabajo como grupo humano. Finalmente la distancia favoreció la decisión ya que yo vivo en la provincia de La Pampa y podría viajar regularmente a tomar los cursos de posgrado ya sea a la UNSL o a la UNRC.

– ¿Cómo fue la experiencia del desarrollo de la Tesis y con acompañamiento virtual de su director?

-En este punto tuve la suerte de cursar la totalidad de los cursos de posgrado de manera presencial, y gran parte de la tesis de maestría fue desarrollada con esta metodología. El hecho de adaptarnos a los encuentros virtuales con el grupo de trabajo para culminar la escritura de la tesis y la posterior presentación de la misma, fue todo un desafío.

Sin embargo, la adaptación forzosa a esta forma de trabajo nos benefició en algunos sentidos, ya que no viajar a cada encuentro nos permitió reuniones más frecuentes, sin el agotamiento físico del viaje. En ese sentido considero que supimos salvar las distancias y esta nueva forma de encontrarnos llegó para quedarse.

– ¿En qué ámbito trabaja actualmente y qué actividad realiza?

-Trabajo como docente de matemática del Departamento de Ciencias Básicas de la Facultad de de Ingeniería de la Universidad Nacional de La Pampa (UNLPam).

-¿Por qué motivos recomienda la formación en esta carrera?

-A todo estudiante del profesorado o la licenciatura en matemática, que realmente le gusta la matemática en sí, le recomiendo el estudio de una carrera de posgrado, en gran parte porque conoce una nueva forma de ver las cosas, se acerca a temas estudiados en la actualidad con desafíos con los que no se ha enfrentado antes. En esta nueva etapa uno debe determinar el camino a seguir, plantear posibles problemas de estudio, ver su factibilidad y enfrentarse a la incertidumbre de no saber si podrá probar la veracidad de sus afirmaciones, encontrar un ejemplo que las refute, o ninguna de ambas. Finalmente una de las cosas más significativas de esta carrera es enfrentarse a estos nuevos desafíos de la mano de un director y un codirector que te ayudan en tu tarea, te orientan y te enseñan a forjar esta nueva forma de pensar, de investigar un tema, cómo es el proceso de escritura de un paper, de una tesis de postgrado y tantas otras cosas que un estudiante desconoce en la carrera de grado. Asimismo, estudiar una carrera de postgrado te invita a conocer un nuevo mundo de personas con los cuales compartir la pasión por una rama de estudio.

Aprovecho este momento para hacer llegar a mi director y co-director mis agradecimientos por acompañarme en la obtención de este nuevo título. Su calidad profesional y humana me han permitido disfrutar de cada parte del proceso, porque sé me acompañan guiando cada uno de mis pasos. También agradecer a la UNSL que tan bien me ha recibido estos años de estudio atendiendo siempre a las necesidades que fueran surgiendo. Por último agradecer a la UNLPam que me brindó las herramientas y el apoyo necesarios para llevar adelante mis estudios de maestría.